
Geometry plays a fundamental role in modern science and engineering. Engineers refine component designs through iterative processes that combine design adjustments with numerical simulations, often to understand how components behave under varying conditions. In aerodynamics, for example, simulations might evaluate a component’s performance as a vehicle travels at a speed of $x$ m/s.
To effectively apply machine learning (ML) and deep learning (DL) in this context, it's essential to develop representations of geometry that are compatible with modern ML/DL techniques.
Decoding Geometry: Unlocking Latent Spaces for 3D Learning
The central challenge in geometric ML/DL lies in representation. Specifically, how to most effectively capture geometry in 3D space using digital formats. Several representations for 3D geometry are commonly used, including discrete formats such as point clouds (sets of points in 3D space), meshes (point clouds enhanced with information about edges and faces that connect the points), and voxels (3D grids of volumetric elements encoding occupancy or other properties).
.png)
There are also functional or implicit representations, such as signed distance functions (SDF), which measure the distance from any point in space to the surface of a geometry. The SDF implicitly defines surface of shapes as the set of points in 3D space, $\Omega$, where the SDF evaluates to zero: $\Omega = \{ \mathbf{x} \in \mathbb{R}^3 : \operatorname{SDF}(\mathbf{x}) = 0 \}$.
While meshes and point clouds are among the most commonly used representations, each has its own limitations, and no universal consensus has emerged on the optimal way to represent geometry for ML.
.png)
A range of ML approaches has been developed to operate on different geometric representations. However, they commonly face challenges such as very high dimensionality in the input space, variable input sizes, architectural complexity, and limited model generalization across representations. Overall, geometric data has proven less amenable to ML compared to tabular or sequential data, where observations are typically represented by scalars, vectors, or matrices — formats that are often the most parsimonious and effective for capturing and utilizing the underlying data.
As mentioned earlier, geometry is a fundamental element of modern engineering and design, where the objective is often to create and manufacture an optimal geometry that meets specific performance goals while satisfying a set of constraints. To evaluate how different designs will perform in the real world, engineers frequently rely on numerical simulation. These simulations typically use mesh-based representations of components. However, during the early design stages, engineers rarely interact directly with meshes. Instead, they work with computer-aided design (CAD) parameterizations that encode key geometric features of the component. From these parameterizations, simulation-ready meshes can be generated. The CAD model introduces a finite set of controllable parameters, degrees of freedom, that can be adjusted to explore design alternatives. In this way, the CAD representation, which is usually much lower in dimensionality than the corresponding simulation mesh, functions as a latent representation of the component’s geometry.
A highly trivial example of this concept in computational geometry can be further illustrated as follows. The image below shows a mesh of a sphere, centered at some location $(x_{c}, y_{c}, z_{c})$, with radius $r$, at increasing resolutions.

As shown, we can represent this sphere at arbitrary levels of detail, using as many points, along with corresponding edges and faces, as desired. However, intuitively, the sphere can also be represented by a latent vector $\mathbf{z}=[x_{c}, y_{c}, z_{c}, r]$, which, assuming the underlying geometry is indeed a sphere, fully captures all relevant information. In this case, the "noise" in the high-dimensional observation arises from the mesh itself and any discretization-specific factors, such as the number and arrangement of points, as well as the arbitrary connectivity between them.

However, CAD parameterizations are not always practical or sufficient for comprehensive design exploration. Creating CAD models is time-consuming and requires specialized expertise, often becoming a bottleneck in the design workflow. Additionally, the fixed nature of a parameterization limits the design space to geometric variations anticipated at the time of model creation. In many cases, particularly when dealing with legacy components or complex organic shapes, a suitable CAD parameterization may not exist at all. Most importantly, the optimal geometry for a given application may lie outside the constrained space defined by the CAD parameters. As a result, even exhaustive exploration within the CAD framework may fail to uncover the best possible design.
This motivates the development of data-driven approaches that can discover similar latent representations directly from geometric data, potentially capturing design patterns and geometric relationships that extend beyond the constraints of traditional parametric modeling.
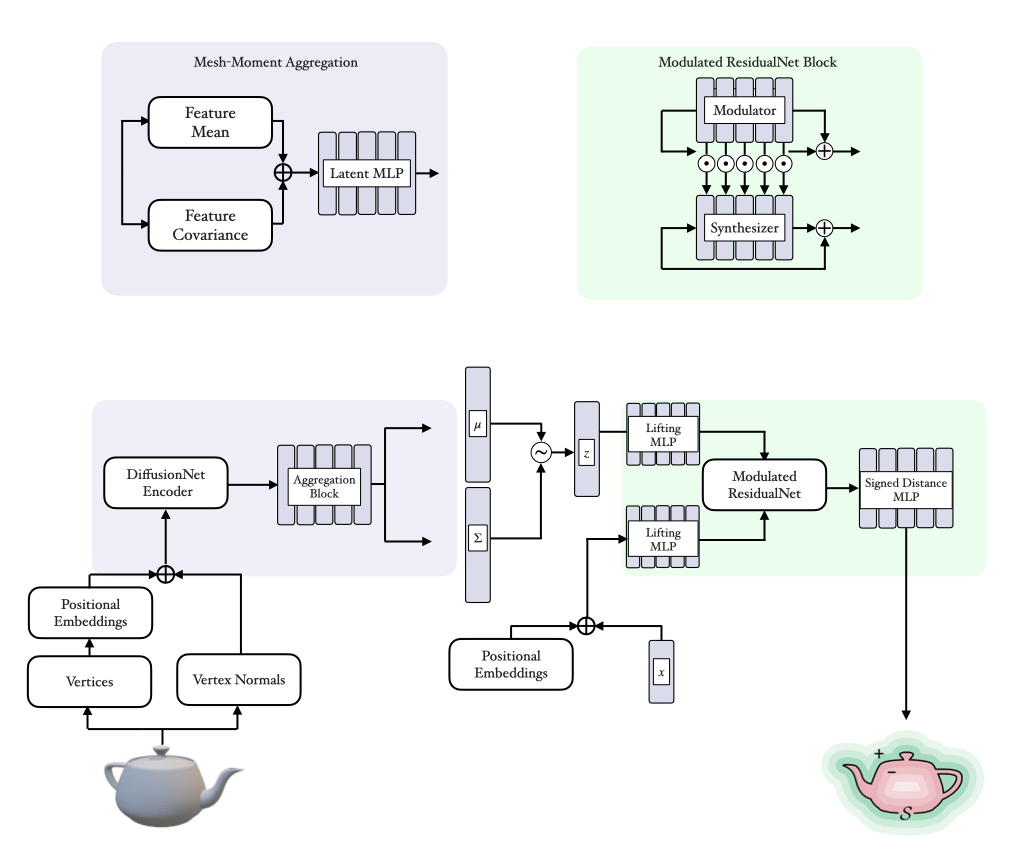
We introduce a variational autoencoder (VAE) architecture, a Large Geometry Model (LGM), designed to map arbitrary high-dimensional mesh-based geometries to compact, lower-dimensional latent representations via an encoder, while enabling accurate reconstruction of the original geometry through a decoder with minimal information loss. This approach builds on the assumption that a low-dimensional, parsimonious representation exists for a set of high-dimensional observations of some underlying geometry, and that it is possible to learn a mapping from these (potentially noisy) high-dimensional measurements to their corresponding latent values. We pre-trained this architecture on tens of millions of geometries to learn effective latent representations across a wide distribution of possible geometries.
Accelerating Design with Surrogate Modeling
To illustrate the benefits of incorporating the LGM into engineering workflows, consider the canonical example of designing a new component. Suppose some company is developing a next-generation widget intended to outperform a previous design. Performance is assessed using a set of scalar metrics, $c_{1}, …, c_{n}$, which are typically derived by integrating some field on the surface of the component calculated from an often slow and expensive numerical simulation. During the design process, the company has generated a set of $N$ candidate geometries for the widget (where generally $N$ is small, i.e., $N < 100$) and has evaluated the scalar metrics for each of these candidates. To accelerate the design cycle, the company now aims to develop an ML-based surrogate model that can predict performance without requiring costly simulations for every new candidate geometry.
A traditional approach to building a surrogate model for this problem involves using the dataset $\{ (\mathcal{G}_{i}, c_{i1}, \ldots, c_{in}) \}_{i=1}^{N}$, where $\mathcal{G}_{i}$ represents a candidate geometry in mesh form. An ML model is then trained to directly consume these meshes and predict one or more scalar targets at the output layer. Typically, this model takes the form of a large neural network, often a graph neural network (GNN), capable of handling the irregular structure and connectivity inherent in mesh data.
However, this direct approach faces several critical limitations, particularly in the small-data regime typical of engineering design. Mesh representations are inherently high-dimensional, often consisting of thousands to millions of vertices, while available training datasets are typically limited in size. This mismatch leads to a severe risk of overfitting, as the model must learn complex mappings from geometry to scalar outputs without sufficient data to effectively constrain the parameter space. Large neural networks, such as GNNs, are also computationally expensive to train and require careful hyperparameter tuning to achieve acceptable performance, making the development of these mesh-based surrogate models time-consuming. Furthermore, when models need to be retrained, either due to additional data becoming available or due to model drift in production (where a model’s predictions deteriorate because the unseen data in production is poorly covered by the training data), the cost of development remains high.
We propose leveraging our pre-trained LGM to reformulate this problem into a more tractable form. Instead of training a surrogate model directly on the high-dimensional mesh data, we first encode each geometry $\mathcal{G}{i}$ into a low-dimensional latent representation $\mathbf{z}_{i} \in \mathbb{R}^{d} \text{ where } d \ll \dim(\mathcal{G}_{i})$. By converting the input geometries into compact latent representations, we can then train a more lightweight ML regressor, such as a Gaussian process (GP), to predict the scalar quantities directly from these latent vectors.
Our surrogate modeling problem can be described as $P(c_{1},...,c_{n}\mid \mathcal{G}_{i})$, where the goal is to predict a set of scalar outputs given a mesh input. Instead of modeling this relationship directly using a mesh-based model such as a GNN, we factor the problem into two stages: $P(c_{1},...,c_{n}\mid \mathbf{z}_{i})P(\mathbf{z}_{i}\mid \mathcal{G}_{i})$. Here, $P(\mathbf{z}^{i} | \mathcal{G}^{i})$ represents the encoder of our pre-trained LGM, which maps the input mesh to a latent vector, $\mathbf{z}_{i} \in \mathbb{R}^{512}$. The second term, $P(c_{1},...,c_{n}\mid \mathbf{z}_{i})$, is the GP (or other lightweight model) mapping from the latent representation to the scalar quantities of interest.
The Benefits of Large Geometry Models
We believe this approach offers several key advantages over the direct mesh-to-scalar method described earlier:
- Reduced Overfitting Risk: Training a GP in a low-dimensional latent space significantly lowers the parameter-to-data ratio, minimizing the overfitting issues that often arise when fitting large neural networks to small datasets.
- Model Simplicity and Computational Efficiency: GPs trained on compact latent vectors require far less computational effort and architectural turning than large neural networks operating on mesh data thus enabling faster iterations during the design cycle and fewer modeling decisions required.
- Built-in Uncertainty Quantification: GPs inherently provide uncertainty estimates for their predictions; in the context of using surrogates this provides confidence intervals for predicted performance metrics on untested designs. This capability supports risk-aware decision-making and helps identify areas where additional simulations would be most beneficial.
- Superior Generalization: The structured latent space learned by the LGM, enforced by the variational aspect of the model and training routine, captures the essential geometric variations that impact performance, effectively filtering out high-frequency noise and mesh-specific artefacts that can confuse direct mesh-based models. This results in improved out-of-sample predictions, which is especially valuable when exploring novel design spaces.
Beyond enhancing surrogate modeling, the latent representation also significantly simplifies the problem of optimizing geometry for some objective. Rather than optimizing thousands of mesh vertices under complex geometric constraints, the company can now focus on modifying a much smaller set of latent parameters: $\mathbf{z}^{*} = \text{argmin}_{\mathbf{z}}\mu_{GP}(\mathbf{z})$.
In other words, this approach allows for more efficient navigation of the input space to identify the latent vector that minimizes (or maximizes) the surrogate model’s ($\mu_{GP}$) prediction for the target quantities. Once the optimal latent vector is identified the decoder reconstructs it into a high-resolution geometry, which can then be validated through numerical simulation and then moved into production.

This lower-dimensional optimization problem is far more tractable than directly optimizing over the mesh, which quickly becomes computationally infeasible due to the high dimensionality of geometric space. Moreover, the GP’s uncertainty estimates can be integrated into acquisition functions for approaches like Bayesian optimization, enabling intelligent and targeted exploration of the design space. To learn more about optimization, see our related article here.
Challenges and Trade-offs
We believe that the LGM and the outlined workflow offer clear advantages over existing approaches for geometric surrogate modeling and design optimization. However, there are important limitations to consider:
- Significant Upfront Investment: Developing a high-quality LGM requires significant investment: months of focused R&D, substantial computational infrastructure, and meaningful financial commitment. At PhysicsX, we made this long-term strategic bet, uniquely positioned to deploy the resulting capability across a range of client organizations and applications. The outcome — transformative value delivered through the advanced workflows this technology unlocks.
- Fine-tuning Requirements for Domain-Specific Applications: Although our LGM was trained on a large and diverse geometric dataset, its latent representations may become noisy or inconsistent when applied to highly specialized or niche geometries that differ significantly from the training distribution. Likewise, very subtle geometric variations might not be fully captured by the model’s learned embeddings. Overcoming these limitations typically requires fine-tuning the autoencoder on application-specific mesh data to generate more accurate latent representations. This process adds complexity, demands additional computational resources, and requires domain expertise as well as access to relevant data.
- Lossy Compression with Autoencoders: The use of an autoencoder, where the model’s output reconstructs the input after passing it through a low-dimensional bottleneck, is closely analogous to traditional compression algorithms. In designing an autoencoder, there is an inherent trade-off between the size of the latent representation and the fidelity of the reconstructed input. Our LGM performs significant compression, prioritizing a compact latent space at the expense of some reconstruction accuracy. By contrast, other geometry models structure their latent spaces differently, often applying little to no compression in order to preserve high-fidelity reconstructions. The dimensionality of the latent space plays a critical role in downstream applications such as surrogate modeling and optimization, making it a key design consideration.
- Strong Assumptions About Latent Space Structure: As a VAE, the LGM enforces a prior distribution on the latent space, embedding specific architectural and distributional assumptions about the geometry’s latent representation. While all Bayesian models require some form of prior, the assumptions imposed by the LGM are particularly strong and can significantly influence model performance. If these assumptions do not align well with the true structure of the geometric domain, the resulting latent representations may be inadequate for the intended tasks. Moreover, diagnosing and correcting such mismatches after training can be challenging.
While we’ve made a strong case for leveraging our LGM in surrogate modeling and geometric optimization, we believe its potential extends far beyond these use cases. There are numerous impactful and innovative applications yet to be explored, each offering new opportunities to deliver value across scientific and engineering domains.
- Geometry Morphing: We believe that having these compact low-dimensional representations of geometry, with the ability to decode back to the high-resolution geometry, could lead to innovations in mesh-morphing over traditional approaches.
- Dynamical Problems: Utilizing the geometric latent space for dynamic and transient problems where geometries evolve over time could be highly impactful in areas like explicit dynamics (i.e., crash modeling) or soft-matter physics.
- Inverse Problems: Our LGM provides a natural framework for solving inverse problems by defining distributions over geometries in the latent space. By using the LGM decoder as the backbone for differentiable geometric forward models, we can efficiently explore the space of possible geometries that are consistent with observed data. This approach leverages the learned geometric priors embedded in the latent representation to regularize the inverse problem and guide the search toward physically plausible solutions.
If you want to work on cutting-edge technology that’s accelerating industrial innovation and transforming how organizations across advanced industries design, build, and operate complex machines and systems — PhysicsX is hiring.

